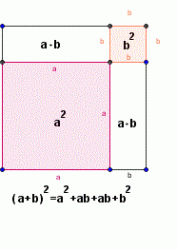
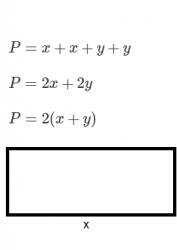Algebra Identities Difference of Squares a2 – b2 = (a-b)(a+b) Difference of Cubes a3 – b3 = (a – b)(a2+ ab + b2) Sum of Cubes a3 + b3 = (a + b)(a2 – ab + b2) Special Algebra Expansions Formula for (a+b)2 and (a-b)2 (a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab +b2 Formula for (a+b)3 and (a-b)3 (a + b)3 = a3 + 3a2b + 3ab2 + b3 (a – b)3 = a3 – 3a2b + 3ab2 – b3 Roots of Quadratic Equation Formula Consider this quadratic equation: ax2 + bx + c = 0 Where a, b and c are the leading coefficients. The…
Category: Algebra Formulas
Mathematics Articles
Scientific Notation
Scientific notation is a convenient way to deal with very large or very small numbers. It provides an easier way to write numbers and make multiplication and division of very large or very small numbers a lot easier. A number is in this format if we can write it as: a × 10n with 1 ≤ a < 10 and n is an integer. 1 ≤ a < 10 means that a is a number between 1 and 10 Thus, a can be 1,2,3,4,5,6,7,8, and 9 Let’s start with something…
Algebra Word Problems
Example of algebra word problems is numerous. The goal of this unit is to give you the skills that you need to solve a variety of these algebra word problems. Example #1: A football team lost 5 yards and then gained 9. What is the team’s progress? Solution For lost, use negative. For gain, use positively. Progress = -5 + 9 = 4 yards Example #2: Use the distributive property to solve the problem below: Maria bought 10 notebooks and 5 pens costing 2 dollars each.How much did Maria pay?…
Calculating the Area and the Perimeter
The perimeter is the length of the outline of a shape. To find the perimeter of a rectangle or square you have to add the lengths of all the four sides. x is in this case the length of the rectangle while y is the width of the rectangle. The perimeter, P, is: P=x+x+y+y P=2x+2y P=2(x+y) Example Find the perimeter of this rectangle: P=7+7+4+4 P=2⋅7+2⋅4 P=2⋅(7+4) P=2⋅11 P=22in The area is measurement of the surface of a shape. To find the area of a rectangle or a square you need…
Solutions of Algebraic Equations
Factoring and Product Formulas
Factoring Formulas a^2 – b^2 = (a-b)(a+b) a^3 – b^3 = (a-b)\left(a^2 + ab + b^2\right) a^3 + b^3 = (a+b)\left(a^2 – ab + b^2\right) a^4 – b^4 = (a-b)(a+b)\left(a^2 + b^2\right) a^5 – b^5 = (a-b)\left(a^4 + a^3b + a^2b^2 + ab^3 + b^4\right) Product Formulas (a + b)^2 = a^2 + 2ab + b^2 (a – b)^2 = a^2 – 2ab + b^2 (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 (a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3 (a + b)^4…
Complex Numbers
Sets of Numbers
Definitions: N : Natural numbers N0 : Whole numbers Z : Integers Z+ : Positive integers Z− : Negative integers Q : Rational numbers C : Complex numbers Formulas: Natural numbers (counting numbers ) N={1,2,3,…} Whole numbers ( counting numbers with zero ) N0={0,1,2,3,…} Integers ( whole numbers and their opposites and zero ) Z={…,−2,−1,0,1,2,…} Z+=N={1,2,…} Z−={…,−3,−2,−1} Z=Z−∪0∪Z Irrational numbers: Non repeating and nonterminating integers Real numbers: Union of rational and irrational numbers Complex numbers: C={x+iy | x∈R and y∈R} N⊂N0⊂Z⊂Q⊂R⊂C