Category: Functions formulas

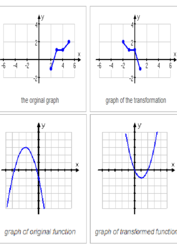
The other exercise type is when you are given two graphs, one being the original function and the other being the transformed function, and you’re asked to figure out the formula for the transformation. The best way I’ve found to approach these it to locate a point that you can clearly track, such as the vertex of a parabola or a turning point (or “bump”) on a cubic. Then try to figure out what that point did. Find a sequence of steps (moving right, sliding down, etc) that works for…

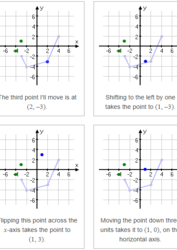
Sometimes you’ll be given a point or a graph with clearly-plotted points, and told to translate the point(s) according to some rule. In other words, they won’t be giving you a function, per se, to move (so you won’t be able to use your graphing calculator to check your work); instead, you’ll be given points to move, and you’ll have to know how to flip them around the axis system yourself. Here’s an example of what that looks like: Given the following graph of f (x), graph the transformation –f (x + 1) – 3 This transformation formula…

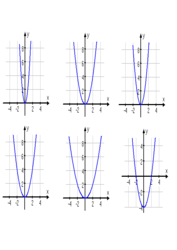
There are two other transformations, but they’re harder to “see” with any degree of accuracy. The first of these transformations is multiplication on the entire function. To see what this looks like, compare the graphs of 2 × f (x) = 2×2, f (x) = x2, and ½ × f (x) = (½) x2, below: graph of 2 × f (x) = 2×2 : (This is skinnier than the regular function’s graph, in the box below.) graph of f (x) = x2 : (This is the graph of the regular function.) graph of ½ × f (x) = (½)x2 :   (This is fatter than the graph of the regular function, which was shown…