The SAT math test is unlike any math test you’ve taken before. It’s designed to take concepts you’re used to and make you apply them in new (and often strange) ways. It’s tricky, but with attention to detail and knowledge of the basic formulas and concepts covered by the test, you can improve your score.
So what formulas do you need to have memorized for the SAT math section before the day of the test? In this complete guide, I’ll cover every critical formula you MUST know before you sit down for the test. I’ll also explain them in case you need to jog your memory about how a formula works. If you understand every formula in this list, you’ll save yourself valuable time on the test and probably get a few extra questions correct.
Formulas Given on the SAT, Explained
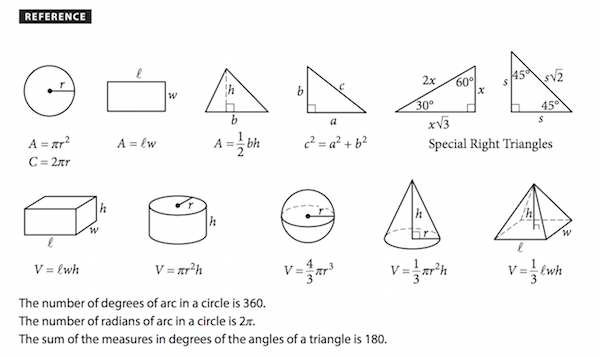
This is exactly what you’ll see at the beginning of both math sections (the calculator and no calculator section). It can be easy to look right past it, so familiarize yourself with the formulas now to avoid wasting time on test day.
You are given 12 formulas on the test itself and three geometry laws. It can be helpful and save you time and effort to memorize the given formulas, but it is ultimately unnecessary, as they are given on every SAT math section.
You are only given geometry formulas, so prioritize memorizing your algebra and trigonometry formulas before the test day (we’ll cover these in the next section). You should focus most of your study effort on algebra anyways because geometry has been de-emphasized on the new SAT and now makes up just 10% (or less) of the questions on each test.
Nonetheless, you do need to know what the given geometry formulas mean. The explanations of those formulas are as follows:
Area of a Circle
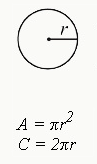
A=πr2
> π is a constant that can, for the purposes of the SAT, be written as 3.14 (or 3.14159)
> r is the radius of the circle (any line drawn from the center point straight to the edge of the circle)
Circumference of a Circle
C=2πr (or C=πd)
> d is the diameter of the circle. It is a line that bisects the circle through the midpoint and touches two ends of the circle on opposite sides. It is twice the radius.
Area of a Rectangle
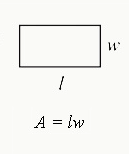
A=lw
> l is the length of the rectangle
> w is the width of the rectangle
Area of a Triangle
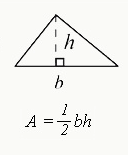
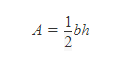
> b is the length of the base of the triangle (the edge of one side)
> h is the height of the triangle
i. In a right triangle, the height is the same as a side of the 90-degree angle. For non-right triangles, the height will drop down through the interior of the triangle, as shown above.
The Pythagorean Theorem
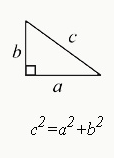
a2+b2+c2
> In a right triangle, the two smaller sides (a and b) are each square. Their sum is equal to the square of the hypotenuse (c, the longest side of the triangle).
Properties of Special Right Triangle: Isosceles Triangle
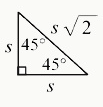
> An isosceles triangle has two sides that are equal in length and two equal angles opposite those sides.
> An isosceles right triangle always has a 90-degree angle and two 45 degree angles.
> The side lengths are determined by the formula: x, x, x√2, with the hypotenuse (the side opposite 90 degrees) having a length of one of the smaller sides *√2.
i. E.g., An isosceles right triangle may have side lengths of 12, 12, and 12√2.
Properties of Special Right Triangle: 30, 60, 90 Degree Triangle
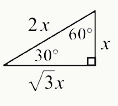
> A 30, 60, 90 triangle describes the degree measures of the triangle’s three angles.
> The side lengths are determined by the formula: x, x√3, and 2x
i. The side opposite 30 degrees is the smallest, with a measurement of x.
ii. The side opposite 60 degrees is the middle length, with a measurement of x√3.
iii. The side opposite 90 degree is the hypotenuse (longest side), with a length of 2x.
iv. For example, a 30-60-90 triangle may have side lengths of 5, 5√3, and 10.
Volume of a Rectangular Solid
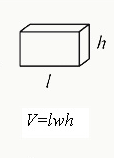
V=lwh
> l is the length of one of the sides.
> h is the height of the figure.
> w is the width of one of the sides.
Volume of a Cylinder
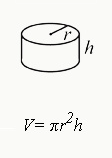
V=πr2h
> r is the radius of the circular side of the cylinder.
> h is the height of the cylinder.
Volume of a Sphere
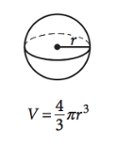
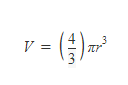
> r is the radius of the sphere.
Volume of a Cone
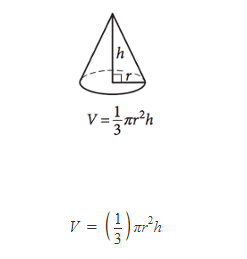
> r is the radius of the circular side of the cone.
> h is the height of the pointed part of the cone (as measured from the center of the circular part of the cone).
Volume of a Pyramid
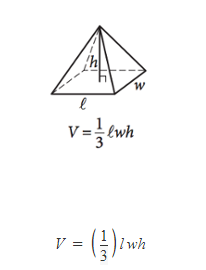
> l is the length of one of the edges of the rectangular part of the pyramid.
> h is the height of the figure at its peak (as measured from the center of the rectangular part of the pyramid).
> w is the width of one of the edges of the rectangular part of the pyramid.
Law: the number of degrees in a circle is 360
Law: the number of radians in a circle is 2π
Law: the number of degrees in a triangle is 180

Gear up that brain because here come the formulas you have to memorize.
Formulas Not Given on the Test
For most of the formulas on this list, you’ll simply need to buckle down and memorize them (sorry). Some of them, however, can be useful to know but are ultimately unnecessary to memorize, as their results can be calculated via other means. (It’s still useful to know these, though, so treat them seriously).
We’ve broken the list into “Need to Know” and “Good to Know,” depending on if you are a formula-loving test taker or a fewer-formulas-the-better kind of test taker.
Slopes and Graphs
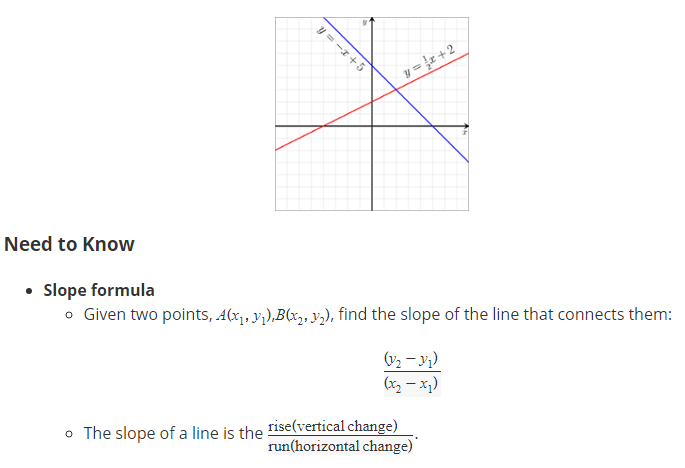
How to write the equation of a line
> The equation of a line is written as:y=mx+b
i. If you get an equation that is NOT in this form (ex. mx−y=b), then re-write it into this format! It is very common for the SAT to give you an equation in a different form and then ask you about whether the slope and intercept are positive or negative. If you don’t re-write the equation into y=mx+b, and incorrectly interpret what the slope or intercept is, you will get this question wrong.
> m is the slope of the line.
> b is the y-intercept (the point where the line hits the y-axis).
> If the line passes through the origin (0,0), the line is written as y=mx.
Good to Know
> Midpoint formula
i. Given two points, A(x1,y1), B(x2,y2), find the midpoint of the line that connects them:
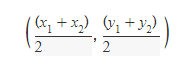
> Distance formula
i. Given two points, A(x1,y1),B(x2,y2), find the distance between them:
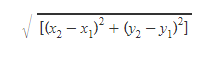
You don’t need this formula, as you can simply graph your points and then create a right triangle from them. The distance will be the hypotenuse, which you can find via the Pythagorean Theorem.
Circles
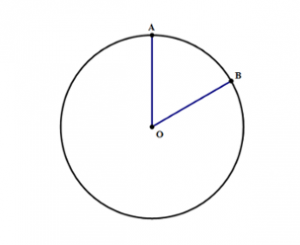
Good to Know
> Length of an arc
i. Given a radius and a degree measure of an arc from the center, find the length of the arc
ii. Use the formula for the circumference multiplied by the angle of the arc divided by the total angle measure of the circle (360)
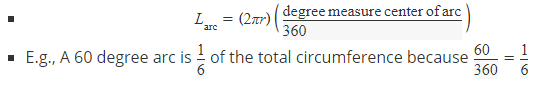
Area of an arc sector
> Given a radius and a degree measure of an arc from the center, find the area of the arc sector
i. Use the formula for the area multiplied by the angle of the arc divided by the total angle measure of the circle
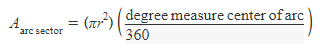


Averages
Need to Know
> The average is the same thing as the mean
> Find the average/mean of a set of numbers/terms
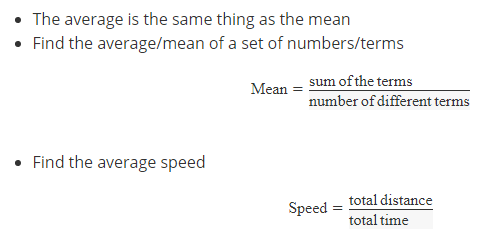
Probabilities
Need to Know
> Probability is a representation of the odds of something happening.
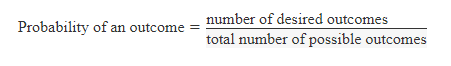
Good to Know
> A probability of 1 is guaranteed to happen. A probability of 0 will never happen.
Percentages
Need to Know
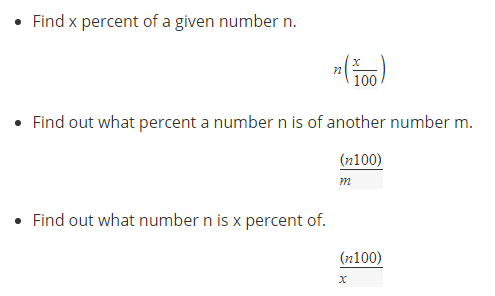
Trigonometry
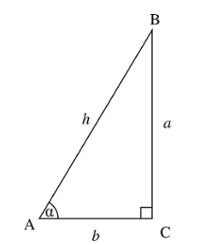
Trigonometry is a new addition to the new 2016 SAT math section. Though it makes up less than 5% of math questions, you won’t be able to answer the trigonometry questions without knowing the following formulas.
