A projectile is an object that is given an initial velocity and is acted on by gravity. The maximum height of the object is the highest vertical position along its trajectory. The maximum height of the projectile depends on the initial velocity v0, the launch angle θ, and the acceleration due to gravity. The unit of maximum height meters (m).
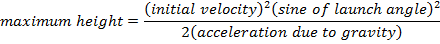
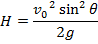
H = maximum height (m)
v0 = initial velocity (m/s)
g = acceleration due to gravity (9.80 m/s2)
θ = angle of the initial velocity from the horizontal plane (radians or degrees)
Maximum Height Formula Questions:
1) A firefighter aims a fire hose upward, toward a fire in a skyscraper. The water leaving the hose has a velocity of 32.0 m/s. If the firefighter holds the hose at an angle of 78.5°, what is the maximum height of the water stream?
Answer: The water droplets leaving the hose can be treated as projectiles, and so the maximum height can be found using the formula:
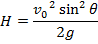
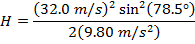
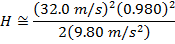
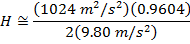
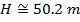
The maximum height of the water from the hose is 50.2 m.
2) An athlete in a high jump competition leaves the ground at a velocity of 5.80 m/s, and an angle of 87.4°. What is the maximum height of the athlete’s center of mass?
Answer: The center of mass of the athlete can be found by treating the person as a projectile, and using the maximum height formula:
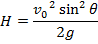
![]()
![]()
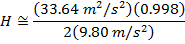
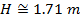
The maximum height of the athlete’s center of mass is 1.71 m.
Note: High jumpers use a technique called the “Fosbury flop” to lower their centers of mass below their bodies. Using this technique means that they can jump over bars approximately 20 cm higher than their centers of mass.