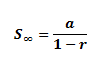Algebra Identities
Difference of Squares
a2 – b2 = (a-b)(a+b)
Difference of Cubes
a3 – b3 = (a – b)(a2+ ab + b2)
Sum of Cubes
a3 + b3 = (a + b)(a2 – ab + b2)
Special Algebra Expansions
Formula for (a+b)2 and (a-b)2
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab +b2
Formula for (a+b)3 and (a-b)3
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
Roots of Quadratic Equation
Formula
Consider this quadratic equation:
ax2 + bx + c = 0
Where a, b and c are the leading coefficients.
The roots for this quadratic equation will be:
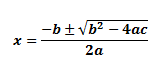
Arithmetic Progression
Consider the following arithmetic progression:
a + (a + d) + (a + 2d) + (a + 3d) + …
Where:
a is the initial term
d is the common difference
The nth term
The nth term, Tn of the arithmetic progression is:
Tn = a + (n – 1)d
Sum of the first n term
The sum of the first n terms of the arithmetic progression is:
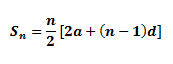
Geometric Progression
Consider the following geometric progression:
a + ar + ar2 + ar3 + …
Where:
a is the scale factor
r is the common ratio
The nth term
The nth term, Tn of the geometric progression is:
Tn = ar n – 1
Sum of the first n terms
The sum of the first n terms, Sn is:
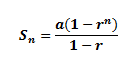
The sum to infinity
If -1 < r < 1, the sum to infinity, S∞ is: